Une courbe verte apparait ; c'est la fonction dérivée de y=cos(x) soit donc y=-sin(x). Attention, le moteur de script n'est pas analytique, il utilise tout simplement la formule de taylor:
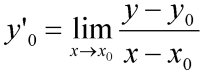
Dans ce premier exemple, nous allons appliquer aux équations cartésiennes vues précédemment un certains nombre de fonctionnalités.
Entrez comme fonction y=cos(x); puis après avoir cliqué
sur le bouton Ajouter de la zone de courbes, entrez la fonction y=derivate(cos(x));
Une courbe verte apparait ; c'est la fonction dérivée de y=cos(x)
soit donc y=-sin(x). Attention, le moteur de script n'est pas analytique,
il utilise tout simplement la formule de taylor:
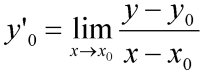
L'aspect de l'écran est le suivant...
Si vous n'êtes pas absolument persuadé de la justesse du résultat, entrez une troisième courbe d'équation y=-sin(x); ... Vous remarquez que cette troisième fonction couvre très exactement la seconde. Voilà un excellent moyen de vérifier votre solution analytique dans le cas d'une dérivée un tant soit peu compliquée.
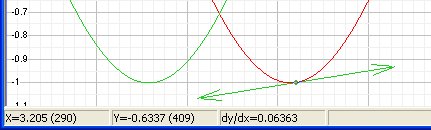
Un autre moyen d'afficher la dérivée sans avoir à créer une fonction particulière est d'appuyer sur la touche F2 (Cliquez éventuellement dans la fenêtre de tracé pour lui donner le focus). Tant que vous maintiendrez cette touche enfoncée, une dérivée de la fonction courante sera affichée en vert dans la zone de visualisation. Un vecteur tangente à la courbe est de plus tracé à la verticale de la position de la souris. La pente en ce point est rappellée dans la barre de status.
Entrez comme fonction y=cos(x); puis après avoir cliqué
sur le bouton Ajouter de la zone de courbes, entrez la fonction y=integral(cos(x));
Une courbe verte apparait ; c'est la fonction y=sin(x) + K; Attention,
le moteur de script n'est pas analytique, il effectue tout simplement un calcul
d'aire sous la courbe. Cette intégrale passe donc par la valeur 0 au
point extrème gauche de la fenêtre de visualisation.
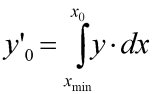
Un décalage de la borne Xmin affecte donc la courbe tracée qui subit donc une translation verticale.
| Un autre moyen d'afficher l'intégrale sans avoir à créer une fonction particulière est d'appuyer sur la touche F3 (Cliquez éventuellement dans la fenêtre de tracé pour lui donner le focus). Tant que vous maintiendrez cette touche enfoncée, l'intégrale de la fonction courante sera affichée en vert dans la zone de visualisation. L'aire calculée est de plus affichée sous forme hachurée à l'écran, et sa valeur est rappellée dans la barre de status. |  |
Note: Si l'expression de y tient en plusieurs instructions comme dans le cas de fonctions définies par parties, terminez votre script par y=Integral(y). L'argument de la fonction Integral doit en effet être une instruction unique.
Entrez comme fonction y=cos(x); Cliquez dans la barre d'outil sur 
.
La fenêtre de log fait apparaître les soultions:
Solution de y=cos(x);
y=1.5708
y=4.7124
Entrez comme fonction y=cos(x); Cliquez dans la barre d'outil sur 
.
La fenêtre de log fait apparaître les extrema:
Extrema de y=cos(x);
(0.0000 , 1.0000)
(3.1416 , -1.0000)
(6.2832 , 1.0000)
Entrez comme fonction y=cos(x); Cliquez dans la barre d'outil sur 
.
La fenêtre de log fait apparaître les intersections:
Points d'inflexion de y=cos(x);
(1.5708 , 0.00000) y'=-1.0000
(4.7124 , 0.00000) y'=1.0000
Entrez comme fonction y=cos(x); Ajoutez les courbes d'équation y=x*x/6-x+1; et e=exp(1); y=ln(x/e); Notez au passage que cette dernière équation commence par définir la constante e avannt d'exécuter le calcul de y. Ceci n'est pas la solution la plus subtile, car e est recalculée pour chacun des points de la courbe, mais ça marche...
Resélectionnez la courbe y=cos(x); Cliquez dans la barre d'outil
sur 
.
La fenêtre de log fait apparaître les points d'intersections:
Intersection(s) entre y=cos(x); et y=x*x/6-x+1;
(0.00000 , 1.0000)
(1.8569 , -0.28223)
(4.6863 , -0.026010)
(5.9417 , 0.94227)
Intersection(s) entre y=cos(x); et e=exp(1); y=ln(x/e);
(1.9238 , -0.34571)
(5.4925 , 0.70343)
Equations
en m